地球流体力学の楽しみ
石岡圭一 (地球物理学教室・准教授)
「専門は何ですか」と聞かれた際,私は「地球流体力学です」と答えることにしています.地球流体力学という分野はあまり一般には知られていないと思いますが,読んで字の如しで,地球(または他の惑星や恒星も含む)に関する流体力学を扱うものです.流体力学については航空機や船舶,またはボールの動き等,日常的に接するものに関連しているので知っている方も多いかと思いますが,では,そこに「地球」が付くと何が違うのと思われるかもしれません.地球流体力学が普通の(工学的な)流体力学と大きく異なっているのは,以下の3つの点においてです.まず 1点目は,地球の自転が流体運動に強い影響を与えるということです.これは主にいわゆるコリオリ力の形で現れます.2点目は,重力の効果です.地球の重力は,大気や海水を地球上から逃がさず保持しているだけでなく,密度の大きいもの程下の方にあるという「密度成層」の状態を作り出しています.このような密度成層があると,浮力を復元力とする波動が生じうるなどの影響があります.3点目は,成分の多様性です.大気中の水蒸気は凝結する際に熱を出してそれが大気の運動に影響を与えますし,海水中の塩分は,その濃度差によって海洋の循環の駆動源になります.このように,地球流体力学には普通の流体力学とは違った面白さがあるだけでなく,研究対象も大気や海洋だけでなく,マントルや外核など,多岐にわたります.
地球流体力学について語り始めると通年の講義をしても全く足りないくらいですので,ここでは,地球自転の効果に絞って,それが流体の運動をいかに常識とは異なる感じに変えてしまうのかということを簡単に説明してみたいと思います.
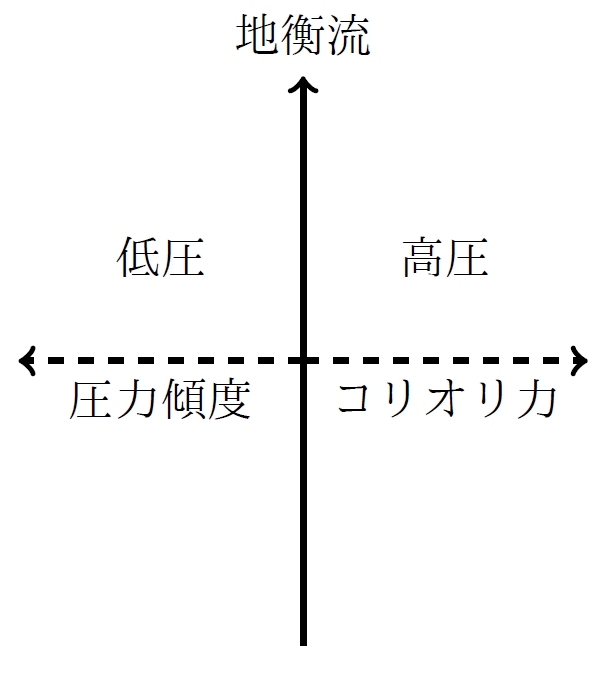
大気や海水のような流体中では,圧力の分布が運動に大きな影響を与えます.圧力が高い場所と低い場所とがあると,高い場所から低い場所に向かう力がはたらきます.これが圧力傾度と呼ばれるもので,管の中の水の流れのように,摩擦力とこの圧力傾度とがつりあっているような状態の場合,圧力が高い方から低い方への流れが生じることになります.ところが,地球のように,回転している系(回転系)の上では,様相が大きく異なってきます.回転系ではコリオリ力と呼ばれる見かけの力がはたらきます.上から見て反時計まわりに回転している台に乗ってボールを投げた場合,台に乗っている人から見ると,ボールが右側カーブして動いていくように見えます.このカーブを引き起こすように見える力がコリオリ力で,この見かけの力の大きさは,ボールの運動の速度に比例し,台の回転の向きが逆なら,力の向きも逆になります.コリオリ力がはたらく地球上で,圧力傾度によってどんな流れが実現するかを考えてみましょう.大気中や海洋中の大規模運動の場合,摩擦の影響は小さいので,圧力傾度とつりあうのはコリオリ力になります.地球の北半球では,上から見ると地表は反時計まわりの回転をしていることになるので,コリオリ力は運動の方向に対して右向きにはたらきます.これと圧力傾度がつりあうので,北半球では図1のように,圧力が高い方を右に見る向きの流れが実現することになります.このように,圧力傾度とコリオリ力とのつりあいによって決まる流れを「地衡流」といいます.地衡流の向きがこのように決まるため,北半球では,高気圧の周りでは時計まわりの,低気圧の周りでは反時計まわりの流れが生じることになります.
地衡流は,圧力傾度に対する向きが日常生活の直感と異なっているだけでなく,もう一つ不思議な性質を持っています.地衡流の向きと流速は,上に述べたように水平方向の圧力傾度によって決まります.任意の深さでの水の圧力は,基本的にその上に載っている水の重さで決まりますので,水平方向の圧力傾度は,水の密度が一定なら深さ方向に変化しません.したがって,地衡流の向きと流速は深さ方向に一様,すなわち水平方向のみに依存し,2次元的となります.地衡流がこのような性質をもつことを示す定理は「テイラー・プラウドマンの定理」と呼ばれ,回転系の流体に対する最も基本的な定理です.
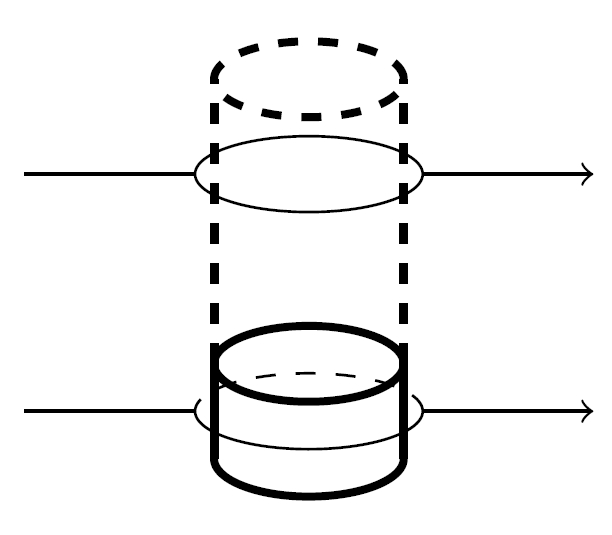
テイラー・プラウドマンの定理によって地衡流が2次元的となることはさらに不思議な現象を引き起こします.水底に障害物がある場合,もし流れがあれば,この障害物のある深さでは,水はこの障害物を迂回して流れなければなりませんが,地衡流が2次元的となる性質によって,障害物の直接の影響を受けない上方でも,障害物の上を迂回するような流れが生じることになります.結局,水底に障害物があると,その影響は上方にも及び,障害物の上の柱上の領域全体が柱状の障害物のようにふるまって流れに影響を与えることになる.この柱状の領域は,「テイラー柱」と呼ばれます(図2).
以上のように系の回転がこれほど流体の影響に大きな影響を与えるというのは,かなり直感に反することもあり,にわかには信じられないかもしれませんが,レコードプレーヤーさえあれば,簡単な実験で確かめることができます.レコードプレーヤーに物を載せるにはターンテーブル中央の突起が邪魔になるので,100円ショップ等で手に入るコルクの鍋敷きやコルクボードに穴を開けたものを載せて,突起が邪魔にならないようにします(図3).その上に,漬物用等に売られている適当な大きさのシール容器に水を入れて載せます(図4).この際,ターンテーブルができるだけ水平になっていることが望ましいので,シール容器中の水面がシール容器内で均一の深さになるように,レコードプレーヤーの足に適当に厚紙を敷くなどして調整しておきます.
この状態で,ターンテーブルを回転させて,容器内の水がターンテーブルの回転と十分に同期するようになるまで待ってから,水の中にスポイトなどで万年筆用のインクを少したらします(ブルーまたはブルーブラックのインクが良いでしょう).インクは水より若干重いので,回転がなければインクが沈みながら広がるだけですが,回転の効果により,インクはカーテン状に広がっていきます(図5).これは,テイラー・プラウドマンの定理によって,水の運動が上下に揃ってしまうためです.
テイラー柱の存在も,次のようにすれば確認することができます.陶器製のプリンカップを空気が入らないように伏せてシール容器中の水の底に沈めます.その状態でターンテーブルを回して,やはり容器内の水がターンテーブルの回転と十分に同期するようになるまで待ってから,プリン用の容器の上を狙ってインクをたらします.すると,テイラー柱の効果により,プリンカップの縁の上を横切るような水の流れが抑制されるため,インクはプリンカップの上からなかなか逃げていくことができず,プリンカップの上だけで円形に広がっていきます.この円形のインクの広がりがテイラー柱に対応することになります(図6).
このように,系の回転の効果は流体の運動に大きな影響を与えます.地球流体力学は,最初に述べたように,回転の効果だけでなく,密度成層の効果や成分の多様性の効果も含んで様々な不思議な振舞いをする流体運動について研究し,現実の大気や海洋等の運動に対する理解を深めていこうとする分野で,理論的な研究から大規模な数値シミュレーションを用いた研究まで幅広いアプローチが可能です.この記事を読んで,少しでも地球流体力学に興味を持っていただけたら幸いです.

 MENU
MENU